Articolo di Goblin Punch del 29 novembre 2012

Introduzione

L'architettura non-euclidea è la pratica di costruire strutture usando la geometria non-euclide. In pratica la parte divertente comincia quando si guarda ad un sistema dove il quinto postulato di Euclide non è vero. Quando ciò accade, si parla di un sistema dove le linee parallele non rimangono sempre alla medesima distanza reciproca.

Ci sono due sistemi basilari per descrivere il non-euclideo: ellittico e iperbolico.

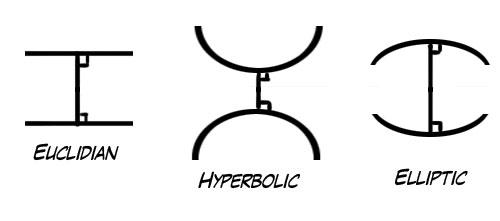
Nella geometria ellittica, due linee parallele prima o poi curveranno l'una verso l'altra (pensate al profilo di una palla da rugby). Lo spazio è curvo, e il grado di tale curva influenza quanto impiegano le linee parallele a intersecarsi e a che angolo lo faranno.

Nella geometria iperbolica è vero l'opposto. Lo spazio è curvo nell'altro senso. Le linee parallele si allontanano tra loro e non si intersecheranno mai, anzi si allontaneranno sempre di più.

La geometria non-euclidea è strana perché sembra spazio normale, così come lo conosciamo, a livello locale. Ma a livello globale è molto diverso.

Ecco un esempio di "localmente normale, globalmente strambo": il globo stesso può essere non-euclideo se assumiamo che la sua superficie sia effettivamente piatta. Un uomo che si trova sull'equatore cammina verso il polo nord. Svolta a 90 gradi a destra e torna verso l'equatore. Svolta ancora a destra di 90 gradi e ritorna da dove'era partito. Se voleste mappare il suo viaggio vi ritrovereste con una figura a tre lati con tre angoli di 90 gradi. Ha fatto un quadrato a tre lati! Se la superficie della terra fosse effettivamente piatta, l'uomo si troverebbe in un luogo non-euclideo (e probabilmente starebbe scappando da qualche aberrazione oscena incontrata al polo nord). 

In realtà la maggior parte dei fisici ritiene che il nostro mondo sia già non-euclideo. Per il fatto che la superficie della Terra è localmente in 2D (e i quadrati sono quadrati) ma esiste in uno spazio a 3D (dove tre angoli retti fanno un triangolo), e l'universo è probabilmente in 3D a livello locale (e i cubi sono cubi) ma a 4D globalmente (e i cubi non sono cubi). 

La Stanza del Pilastro

Come si applica tutto ciò al tavolo da gioco? Lasciate che vi introduca la Stanza del Pilastro.

Immaginate di entrare in una stanza con un pilastro a base quadrata nel centro. Camminate attorno al pilastro per tutti e 360 i gradi, e notate che ha quattro lati con angoli di 90 gradi negli spigoli, e completato il giro vi ritrovate al punto d'inizio. Tutto normale, no? Una stanza normale. Ma che succede se vi tocca girare attorno al pilastro per più di 360 gradi? Che succede se dovete camminarci attorno due volte, impiegando 720 gradi per tornare alla porta?

Immaginatelo così: il gruppo entra nella stanza dall'unica porta (sul muro Sud). Il ladro decide di girare attorno al pilastro per guardarsi attorno, ma quando torna indietro alla parete Sud, il gruppo è scomparso. Il ladro può ancora sentire il resto del gruppo che gli chiede perché si sta nascondendo dietro al pilastro (il suono rimbalza sulla parete Nord), ma non può sentirli. Infatti, anche la porta è scomparsa, anche se sta guardando proprio la parete Sud. Gli basta però percorrere altri 360 gradi attorno al pilastro (in un senso o nell'altro) per tornare da loro. 

Con l'architettura non-euclidea, una stanza di 3x3m può contenere 18m quadrati.

Potete notare come ciò sia molto simile all'iperspazio, con molte cose che occupano il medesimo spazio. Infatti la stanza che ho appena descritto può essere duplicata mettendo un portale discreto a due direzioni che si estende dal "retro" del pilastro a metà della parete Nord. Questo portale porterebbe da una stanza identica alla prima (che non ha però una porta, e ovviamente non ha una copia del resto del gruppo). Camminando attorno al pilastro il ladro si troverebbe a camminare attraverso al portale fino a raggiungere la stanza identica senza nemmeno accorgersene. Un altro giro di 360 gradi attorno al pilastro lo riporterebbe indietro.

Ma questa è roba semplice.

E se per tornare al punto di partenza fossero necessari solo 270 gradi? Il ladro girerebbe attorno a 3/4 del pilastro prima di tornare al resto del gruppo, anche se il pilastro ha degli spigoli quadrati. Infatti il ladro potrebbe trovarsi nello spigolo Nord-Ovest della stanza (dopo aver lasciato il gruppo vicino alla parete Sud) e vedere il gruppo in due posti diversi. E il gruppo vedrebbe due ladri. Nota: non stanno vedendo delle copie, stanno effettivamente guardando il ladro da due direzioni perché lo spazio è curvo e le linee parallele si incontrano in quel punto. Questa è una geometria ellittica e la stanza apparentemente quadrata in realtà ha tre angoli. Questa è una stanza di 3x3m ma ha un'area di 6m quadrati. 

Se per girare attorno al pilastro fossero necessari 180 gradi, il pilastro sarebbe un quadrato a due facce, e il ladro potrebbe fare cose davvero assurde come pugnalarsi alla schiena da solo mentre sbircia oltre all'angolo. Gli spazi altamente ellittici diventano bizzarri molto in fretta, e ne parleremo a breve.

Ma cosa succederebbe se lo spazio fosse altamente iperbolico? Cosa succede se ti tocca camminare attorno al pilastro per dieci volte prima di tornare da dove sei venuto? Una stanza di 3x3m potrebbe improvvisamente 92m quadri, con un pilastro quadrato a 40 facce.

E se mettete due pilastri di questo tipo nella stanza, e la chiamate un labirinto? A seconda di come il gruppo si muove attorno ai due pilastri, potrebbero perdersi molto in fretta, oppure arrivare molto in fretta alla porta dalla quale sono entrati. Una stanza di 3x6m con due pilastri potrebbe essere... dannazione, grande quanto volete, con tante diramazioni quante ne volete voi. Se mettete un mostro in una stanza a due pilastri, il gruppo potrebbe trovarsi costantemente a 6m dal mostro, in ogni momento. Ci sarebbe un baccano come in un gigantesco impianto di smaltimento dei rifiuti, e il gruppo griderebbe come un gruppo di cheerleader, ma né il gruppo né il mostro riuscirebbe a capire come raggiungere la parte opposta (dato che i rumori vengono da tutte le direzioni). Spaventoso, vero?

Suggerimento divertente: quando cercate di mappare un semplice labirinto iperdimensionale, pensate a ciascun centro della stanza come ad un singolo luogo. Poi cercate di capire dove vi porterà ciascuna delle possibili direzioni da prendere (ciascuna direzione attorno al pilastro) e a quale luogo vi condurrà. Solo perché confonderà i vostri giocatori, non significa che debba confondere anche voi!

Ora è il momento di pensare in grande.

Non fatevi spaventare dall'idea di estrapolare l'idea della stanza del pilastro e applicarla all'intero dungeon. Magari un giro attorno al pilastro vi porta ad un dungeon molto simile: il gruppo potrebbe non accorgersi della differenza, almeno per un po', e non si renderà conto che il pilastro potrà portarli indietro.

Ora immaginatevi una stanza principale posta tra due pilastri, come nel labirinto a due pilastri. A seconda di dove vi trovate nel labirinto, la stanza centrale potrebbe avere temi o scopi differenti. Potete far stare un dungeon di venti stanze in un'area di 15x15m. Il pilastro non deve nemmeno essere un pilastro. Può essere un corridoio quadrato, nel quale il gruppo deve camminare tre volte prima di tornare al punto di partenza (questo corridoio ha tre sale nord, tre sale est, tre sale sud e tre sale ovest). Può essere un pozzo nel quale il gruppo deve saltare, cadendo in acqua. Può essere un arco di trionfo, oppure la tana di un topo. Forse è un edificio, dove le finestre frontali conducono ad un luogo diverso della porta frontale. Può essere un gazebo. 

Infine avete la possibilità di creare delle mappe davvero senza senso. Se cinque svolte di 90 gradi a sinistra equivalgono ad una svolta a destra, potete benissimo mettere due stanze nello stesso spazio e confondere i tentativi dei personaggi di creare una mappa sensata.

Interfacciare spazi non-euclidei con spazi euclidei

Non potete. Appena cominciate a mettere in campo quadrati a tre lati, cominciate a incappare in alcuni problemi. Tecnicamente dovreste mappare questi spazi usando strane tassellazioni e non carta quadrettata. Ma gli spazi non-euclidei possono funzionare bene in spazi confinati come l'interno di un'astronave o di un dungeon, dove sono limitati dagli ingressi e dalle uscite delle singole stanze. Potete divertirvi un mondo a mappare una stanza non-euclidea. Il trucco è ricordarsi che localmente lo spazio è localmente euclideo (i quadrati sono percepiti ancora come quadrati), ma non lo è su grande scala (un quadrato abbastanza grande non ha più quattro lati).

Cominciate in modo semplice. Magari un giro attorno ad un pilastro conduce ad un corridoio che curva in modo diverso da quello con il quale i personaggi sono entrati nella stanza, e conduce ad un luogo diverso. Magari camminare in senso orario porta a versioni sempre più vecchie della nave, finché al quarto giro vi ritrovate ad un vicolo cieco, in una nave praticamente derelitta (e magari, se volete rendere la cosa stupida, il personaggio ha pure viaggiato indietro nel tempo).

E se il vostro gruppo comincia a buttare giù i muri tra spazi euclidei e non-euclidei... beh, rompere qualcosa che tiene assieme un oggetto impossibile non è certo una cosa intelligente. Alcune opzioni per il DM includono (ma non sono limitate a): esplosioni (per lo spazio iperbolico), implosioni (per quello ellittico), vortici risucchianti, turbamenti senzienti, Cthulhu, etc.